
| Address: |
5321, James Clerk Maxwell Building Peter Guthrie Tait Road Edinburgh, EH9 3FD |
|---|---|
| E-mail: |
obusani (at) ed.ac.uk ofer659 (at) gmail.com |
I am a Lecturer (assistant professor) at the University of Edinburgh. I am mainly interested in probabilistic models that have strong connections to statistical physics.
In particular, I am interested in the Kardar–Parisi–Zhang (KPZ) universality class where one can find random growth processes, interacting particle systems, random polymers, stochastic PDEs and many other interesting models.
Open positions
I will have two openings this year funded by the ERC Starting Grant UnivKPZ.
PhD Position (4 years)
Start 2026–27Interested applicants should apply via the University portal and mention in the application that they'd like to work with me. The student will work on central open problems in the KPZ class.
Apply for the PhDPhD students
Zhicheng Zheng — PhD (2025)
The KPZ Universality Class
Many natural processes involve random growth and fluctuation. Think of moss spreading on a rock, frost crystals forming on a window, or a coffee stain drying into irregular patterns. In each case, an interface—the edge between the grown region and the untouched one—evolves over time in a way that is both systematic and random.
Mathematicians and physicists discovered that a surprisingly broad range of such growth processes behave in a universal way: despite very different microscopic rules, their large-scale shapes and the statistics of their fluctuations fall into the same “family.” This family is called the Kardar–Parisi–Zhang (KPZ) universality class (1986).
“Universal” here means that once we look on the right space–time scales, very different systems—traffic flow, bacterial colonies, flame fronts, crystal growth, and more—exhibit the same limiting behavior for shape and fluctuations, captured by common mathematical structures.
Why do we need KPZ models?
KPZ models act as a mathematical laboratory for complex random systems. Real-world growth is often too messy to analyze directly, but simplified KPZ-type models capture the essential features while remaining tractable. Studying them helps us:
- Predict large-scale behavior of physical, biological, and engineered growth processes.
- Uncover universal laws that apply across seemingly unrelated systems.
- Develop tools in probability, analysis, and random matrices that inform other areas of science.
To get a better feel for what a model in the KPZ class is, let us look at a very classical example: the corner growth model (CGM). We place ourselves on the lattice \(\mathbb{Z}^2\), rotated by \(45^\circ\). At time zero, we declare some sites to be infected (blue vertices) while the rest remain healthy (black vertices). Each site of the lattice is assigned a random weight, such that the weights are independent and identically distributed across the lattice. The dynamics are simple to describe: a site becomes eligible for infection (the purple vertices) once both of the sites directly below it are already infected. At that moment, we wait for a period of time equal to its random weight, after which the site itself flips from healthy to infected. This iterative mechanism drives the infection forward and produces the evolving random growth that we want to study.
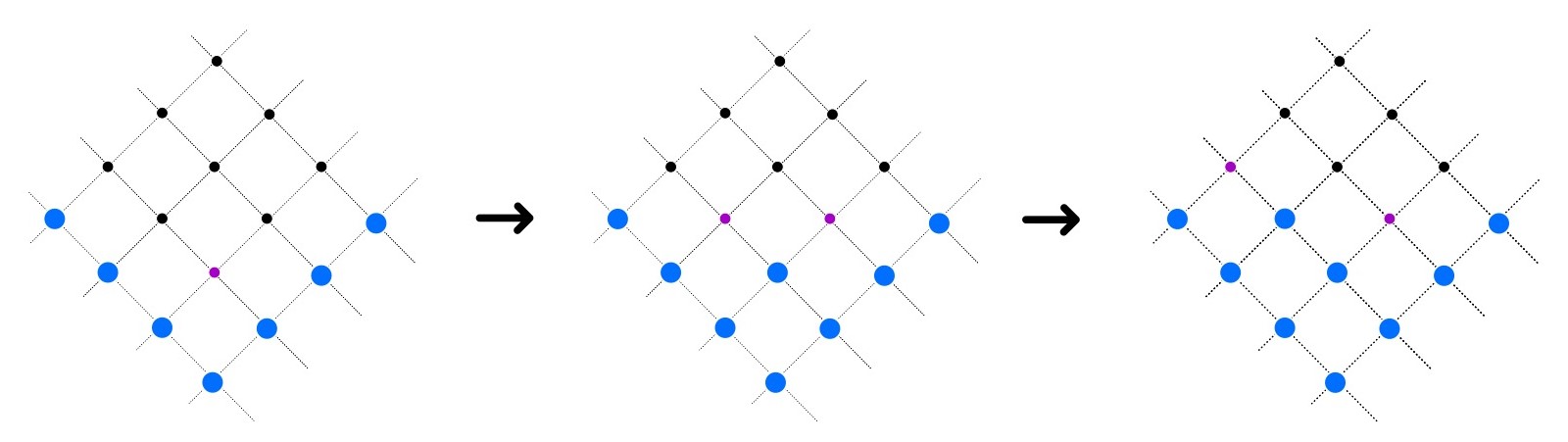
A few natural questions arise at this point. Starting from a given infected set, should we indeed see the emergence of a macroscopic shape (shown below in red) as time grows? What can we say about the properties of this shape? Beyond that, what can be said about the scale of the fluctuations around it — in other words, how closely must we zoom in (what are the relevant dimensions of the rectangle below) in order to observe non-trivial random behaviour?
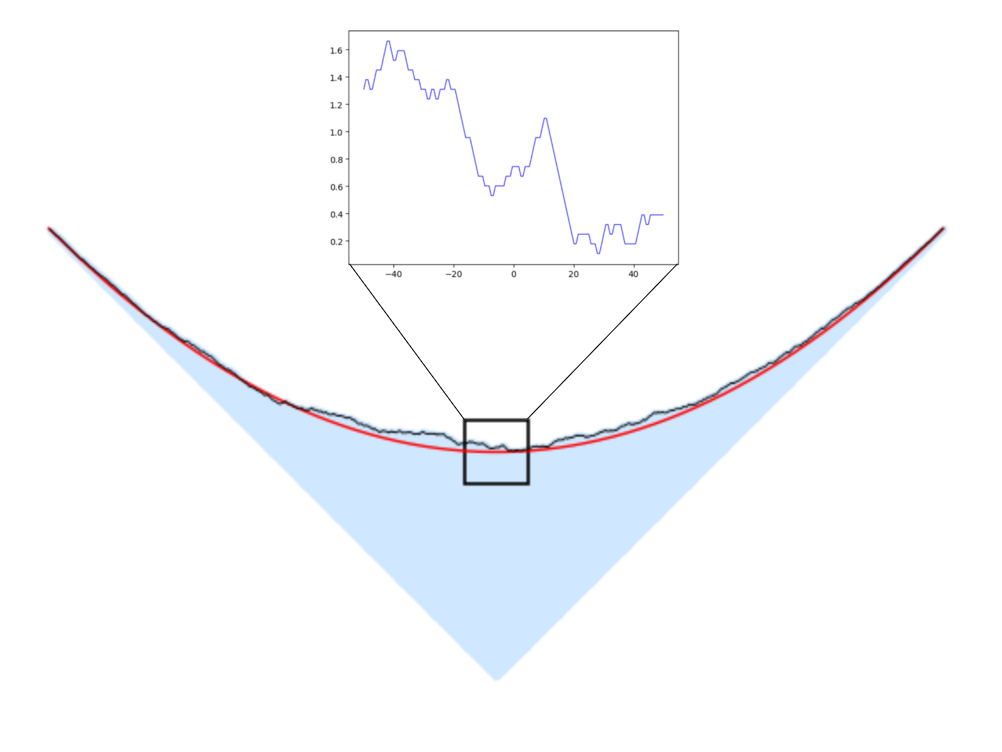
Corner Growth Model Simulation
Papers and Preprints
- With Sudeshna Bhattacharjee and Evan Sorensen Exceptional force, uncountably many solutions in the KPZ fixed point arXiv:2505.09604. 2025.
- With Gideon Amir, Christophe Bahadoran and Ellen Saada Hydrodynamics and relaxation limit for multilane exclusion process and related hyperbolic systems. arXiv:2501.19355. 2025.
- With Kazumasa A. Takeuchi, Jacopo De Nardis, Patrik L. Ferrari and Romain Vasseur Partial yet definite emergence of the Kardar–Parisi–Zhang class in isotropic spin chains. Physical Review Journal. 2024.
- Non-existence of three non-coalescing infinite geodesics with the same direction in the directed landscape. arXiv:2401.00513. 2023
- With Timo Seppäläinen and Evan Sorensen Scaling limit of multi-type invariant measures via the directed landscape. International Mathematics Research Notices. 2024.
- With Timo Seppäläinen and Evan Sorensen Scaling limit of the TASEP speed process. Ann. Inst. Henri Poincaré Probab. Stat.. 2022.
- With Riddhipratim Basu and Patrik Ferrari On the exponent governing the correlation decay of the Airy1 process. Communications in Mathematical Physics. 2022.
- With Timo Seppäläinen and Evan Sorensen The stationary horizon and semi-infinite geodesics in the directed landscape. Annals of Probability. 2022.
- Diffusive scaling limit of the Busemann process in Last Passage Percolation. Annals of Probability. 2021
- With Gidi Amir, Christophe Bahadoran, Ellen Saada Invariant measures for multilane exclusion process. Ann. Inst. Henri Poincaré Probab. Stat.. 2021
- With Timo Seppäläinen Non-existence of bi-infinite polymer Gibbs measures. Electronic Journal of Probability. 2022
- With Timo Seppäläinen Bounds on the running maximum of a random walk with small drift. ALEA. 2022
- With Patrik L. Ferrari Universality of the geodesic tree in last passage percolation. Annals of Probability. 2020
- With Marton Balazs, Timo Seppäläinen Local stationarity of exponential last passage percolation. Probability Theory and Related Fields. 2021
- With Gidi Amir, Patricia Goncalves, James Martin The TAZRP speed process. Ann. Inst. Henri Poincaré Probab. Stat.. 2019
- With Marton Balazs, Timo Seppäläinen Non-existence of bi-infinite geodesics in the exponential corner growth model. Forum of Mathematics, Sigma. 2020
- Continuous Time Random Walk as a Random Walk in Random Environment. arXiv:1709.02141. 2018
- Finite dimensional Fokker-Planck equations for continuous time random walk limits Stochastic Processes and their Applications. 2017
- Aging Uncoupled Continuous Time Random Walk Limits Electronic Journal of Probability. 2016
Contributions
- On the number of infinite geodesics in last passage percolation models. To appear in “From Particle Systems to Partial Differential Equations”. Proceedings of PSPD XII.